深入探究ECDHE算法

一、加密与数论基础

在正式谈及 ECDHE 之前，需要先谈谈与之关系紧密的 RSA 算法。ECDHE 是建立在优化 RSA 部分特性的前提下诞生的。

1.1 非对称加密

RSA算法 常应用于非对称加密，非对称加密生成一对密钥，常见的使用场景为：

• 公钥加密，私钥解密。这个目的是为了保证数据传输安全性，因为被公钥加密的内容，其他人是无法解密的，只有持有私钥的人，才能解密出实际的内容；
• 私钥加密，公钥解密。这个目的是为了保证数据真实性，因为私钥是不可泄露的，如果公钥能正常解密出私钥加密的内容，就能证明这个消息是来源于持有私钥身份的人发送的。

想要理解 RSA算法，首先需要从几个初等数论概念着手。

1.2 素数

素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。 比如：2、3、5、7、11、13、17、19 … 而素数已被证明有无穷多个，共有6种证法（分别为 欧几里得法，埃尔米特法，戈德巴赫法，弗斯滕伯格法，菲利普法），其中 欧几里得法 最为经典，论证过程可参考《几何原本》第9卷。

1.3 模运算

模运算：即 求余运算，指一个数除以另一个数，不够除的部分就是余数，就是求余的结果。

同余：当两个整数除以同一个正整数，若得相同余数，则二整数同余。 设两个整数a，b，若它们除以 正整数m 所得的余数相等，则称a，b对于 模m 同余，记作：

$$a \equiv b \setminus \pmod{m}$$

读作：a 同余于 b 模 m，或者，a与b 关于 模m 同余。例如：

$$26 \equiv 14 \setminus \pmod{12}$$

1.4 互质关系

如果两个正整数，除了1以外，没有其他公因子，称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

根据互质关系，可推结论：

• 任意两个质数构成互质关系，比如13和61。
• 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。
• 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。
• 1和任意一个自然数是都是互质关系，比如1和99。
• p是大于1的整数，则p和p-1构成互质关系，比如57和56。
• p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

1.5 欧拉函数

求证：任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？

计算互质关系数量的方法就叫做欧拉函数，以φ(n)表示。比如在1到8之中，与8形成互质关系的是1、3、5、7，那么 φ(n) = 4。欧拉函数分为5种情况：

情况一：如果n=1，则 φ(1) = 1 。

因为1与任何数（包括自身）都构成互质关系。

情况二：如果n是质数，则 φ(n) = n-1 。

因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

情况三：如果n是质数p的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则

$$\phi(p^{k})=p^{k}-p^{k-1}$$

这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1)个，即1×p、2×p、3×p、…、p^(k-1)×p，把它们去除，剩下的就是与n互质的数。比如

$$\phi(8)=\phi(2^{3})=2^{3}-2^{2}$$

上面的式子还可以写成下面的形式：

$$\phi(p^{k})=p^{k}-p^{k-1}=p^{k}(1-\frac{1}{p} )$$

可以看出，上面的 情况二 是 k=1 时的特例。

情况四：如果n可以分解成两个互质的整数之积，n = p1 × p2，则

$$\phi(n)=\phi(p1p2)=\phi(p1)\phi(p2)$$

即积的欧拉函数等于各个因子的欧拉函数之积。比如

$$\phi(56)=\phi(8×7)=\phi(8)\phi(7)=4x6=24$$

具体证明可参考 “中国剩余定理”。

情况五：

因为任意一个大于1的正整数，都可以写成一系列质数的积。

$$n=p_{1}^{k1}p_{2}^{k2}...p_{r}^{kr}$$

根据 情况四 的结论，得到

$$\phi(n)=\phi(p_{1}^{k1})\phi(p_{2}^{k2})...\phi(p_{r}^{kr})$$

再根据 情况三 的结论，得到

$$\phi(n)=\phi(p_{1}^{k1})\phi(p_{2}^{k2})...\phi(p_{r}^{kr})(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})...(1-\frac{1}{p_{r}})$$

也就等于

$$\phi(n)=n(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})...(1-\frac{1}{p_{r}})$$

以上便是 欧拉函数的通用计算公式。

1.6 欧拉定理

如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

$$a^{\phi (n)} \equiv 1 \pmod{n}$$

也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。这就是著名的欧拉定理。

比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

欧拉定理可以大大简化某些运算。比如，7和10互质，根据欧拉定理，

$$7^{\phi (10)} \equiv 1 \pmod{10}$$

已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。

$$7^{\phi (4k)} \equiv 1 \pmod{10}$$

因此，7的任意次方的个位数（例如7的222次方），心算就可以算出来。

欧拉定理有一个特殊情况：

假设正整数a与质数p互质，因为质数p的 φ( p ) 等于p-1，则欧拉定理可以写成

$$a^{p-1} \equiv 1 \pmod{p}$$

这就是著名的费马小定理。它是欧拉定理的特例。

欧拉定理是RSA算法的核心。理解了这个定理，就可以理解RSA。

1.7 模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1。

$$ab \equiv 1 \pmod{n}$$

这时，b就叫做a的 “模反元素”。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即：

如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

$$a^{\phi (n)}=a * a^{\phi (n)-1} \equiv 1 \pmod{n}$$

可以看到，a的 φ(n)-1 次方，就是a的模反元素。

二、从RSA说起

普及完上述的数论定理，接下来正式展开 RSA算法 的细节。

2.1 RSA简易数学模型

假设 Smallfan 要使用 RSA算法 和 Jenning 进行加密通信，那么他需要生成公钥和私钥步骤如下：

第一步，随机选择两个不相等的质数p和q。

假设选择了3和11。（实际应用中，这两个质数越大，就越难破解。）

第二步，计算p和q的乘积n。

$$n = 3*11 = 33$$

n的长度就是密钥长度。33写成二进制是100001，一共有6位，所以这个密钥就是6位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

第三步，计算n的欧拉函数φ(n)。

∵ n是质数，根据欧拉函数可知
φ(n) = n-1
n = p1 × p2
φ(n) = φ(p1p2) = φ(p1)φ(p2)
∴ φ(n) = (p-1)(q-1)

$$\phi (33)=2 * 10 = 20$$

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

假设在1到20之间，随机选择了17。

第五步，计算e对于φ(n)的模反元素d。

所谓”模反元素”就是指：有一个整数d，可以使得ed被φ(n)除的余数为1。

$$ed \equiv 1 \pmod{\phi(n)}$$

这个式子等价于

$$ed - 1 = k\phi(n)$$

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解。(-k = y)

$$ex + \phi(n)y = 1$$

已知 e=17, φ(n)=20，

$$17x + 20y = 1$$

根据 “扩展欧几里得算法” 求得整数解为 (x,y) = (-7, 6)，即 d = -7。

第六步，将n和e封装成公钥，n和d封装成私钥。

n=20，e=17，d=-7，所以公钥就是 (20,17)，私钥就是（20, -7）。

注意：实际应用中，公钥和私钥的数据都采用 ASN.1 格式表达。

2.2 加密和解密

2.2.1 加密

回到上面的场景，假设 Jenning 要向 Smallfan 发送加密信息m，她就要用 Smallfan 给出的公钥 (n,e) 对m进行加密。这里需要注意，m必须是整数（字符串可以取ascii值或unicode值），且m必须小于n。

所谓”加密”，就是算出下式的c：

$$m^{e} \equiv c \pmod{n}$$

Smallfan 的公钥是 (20, 17)，m假设是2，那么可以算出下面的等式：

$$2^{17} \equiv 12 \pmod{20}$$

于是，c等于12， Jenning 就把 12 发给了 Smallfan 。

2.2.2 解密

Smallfan 拿到 Jenning 发来的 12 以后，就用自己的私钥 (20, -7) 进行解密。可以证明，下面的等式一定成立：

$$c^{d} \equiv m \pmod{n}$$

也就是说，c的d次方除以n的余数为m。现在，c = 12，私钥是(20, -7)，那么

$$12^{-7} \equiv 2 \pmod{20}$$

因此，加密前的原文就是 2。

至此，”加密–解密”的整个过程全部完成。

具体求证过程，可参考阮老师的 RSA算法原理（二）

2.2.3 长内容加密

公钥 (n,e) 只能加密小于n的整数m，那么如果要加密大于n的整数，该怎么办？有两种解决方法：

1. 把长信息分割成若干段短消息，每段分别加密；
2. 先选择一种”对称性加密算法”（比如DES），用这种算法的密钥加密信息，再用RSA公钥加密DES密钥。

2.3 可靠性分析

回顾上面的密钥生成步骤，一共出现六个数字：

随机生成的两个质数p和q
p和q的乘积n
欧拉函数φ(n)
随机生成的1-φ(n)区间内的与φ(n) 互质的整数e
e的模反元素d

这六个数字之中，公钥用到了两个（n 和 e），其余四个数字都是不公开的。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。

做个假设：在已知n和e的情况下，能否推导出d？

∵ ed≡1 (mod φ(n))。∴ 知道 e 和 φ(n)，才能算出 d。
∵ φ(n) = (p-1)(q-1)。∴ 知道 p 和 q，才能算出 φ(n)。
∵ n = pq。∴ 将 n 因数分解，才能算出 p 和 q。

结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

举例来说，你可以对33进行因数分解（3×11），但是很难对下面这种比较大的整数进行因数分解。

1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413

它等于这样两个质数的乘积：

33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489
×
36746043666799590428244633799627952632279158164343087642676032283815739666511279233373417143396810270092798736308917

注意：截止到2023年，目前业界普遍认为：RSA 1024已经普遍不安全，根据当前的算力模型预测，有生之年很快就会被破解，而量子计算机的引入无疑加速了这一切。

目前有不同的算力模型，因此每种模型下给出的预测结果都是不同的，但是总的来看的话基本上都认为 1024bit 的 RSA 已经不适合使用了。

• Lenstra / Verheul 模型得出 1007-1028bit RSA 在 2002-2006 年左右就不安全了。
• ECRYPT-CSA 模型得出 1024bit RSA 在 2010-2017 年左右就不安全了。
• NIST 模型认为 1024bit RSA 在 2016 年之后就不安全了。
• ANSSI 模型认为 2048bit RSA 将在 2014-2020 年左右变为不安全。
• BSI 模型认为 2000bit RSA 将在 2018-2022 年左右变为不安全。

不同的算力模型的结论可以在 keylength.com/en/ 这个网站查询。

2.4 前向安全性问题

正如可靠性分析部分所述，目前RSA被暴力破解的可能性较高，另外由于在HTTPS实际应用场景中，私钥常存放于服务端，持有私钥的开发人员、运维人员等可能有意无意会造成私钥的泄露。一旦服务端的私钥泄漏了，过去被第三方截获的所有 TLS 通讯密文都会被破解。这就是 RSA最大的缺陷：不具备前向安全性。

为此，HTTPS逐步过渡采用一个动态、可靠、离散的私钥协商方法，即本文重点：ECDHE算法。

三、离散对数

3.1 基本定理

ECDHE 密钥协商算法是 DH 算法演进过来的，DH 算法基于 离散对数 。

离散对数是「离散 + 对数」的两个数学概念的组合。对数运算的取值是可以连续的，而离散对数的取值是不能连续的，因此也以「离散」得名，离散对数是在对数运算的基础上加了「模运算」，也就说取余数。

如果对于一个整数 b 和质数 p 的一个原根 a，可以找到一个唯一的指数 i，使得：

$$a^{i} \bmod{p} = b$$

那么指数 i 称为 b 的 以 a 为底数的模 p 的离散对数。

3.2 模数P的明确

底数 a 和模数 p 是离散对数的公共参数，也就说是公开的，b 是真数，i 是对数。知道了对数，就可以用上面的公式计算出真数。但反过来，知道真数却很难推算出对数。

根据欧拉定理证明部分可知，当模数 p 是一个大数，即使知道底数 a 和真数 b ，以现有计算水平很难算出离散对数，这就是 DH 算法的数学基础。

关于 质因分解 和 真数反推对数 可阅读本文第七章。

四、DH与DHE算法

4.1 基于DH的对称密钥生成

现假设 Jenning 和 Smallfan 约定使用 DH 算法来交换密钥，那么基于离散对数， Jenning 和 Smallfan 需要先确定模数 P 和底数 G 作为算法的参数，这两个参数是公开的。

然后 Jenning 和 Smallfan 各自生成一个随机整数作为私钥，双方的私钥要各自严格保管，不能泄漏， Jenning 的私钥用 a 代称， Smallfan 的私钥用 b 代称。

现在 Jenning 和 Smallfan 双方都有了 P 和 G 以及各自的私钥，于是就可以计算出公钥：

• Jenning 的公钥记作 A，

$$A = G^{a} \bmod{p}$$

• Smallfan 的公钥记作 B，

$$B = G^{b} \bmod{p}$$

A 和 B 也是公开的，因为根据离散对数的原理，从真数（A 和 B）反向计算对数 a 和 b 是非常困难的。

双方交换各自 DH 公钥后，双方的持有情况如下：

Jenning 手上共有 5 个数：P、G、a、A、B
Smallfan 手上也同样共有 5 个数：P、G、b、A、B

然后 Jenning 执行运算：

$$K_{1} = B^{a} \bmod{p}$$

Smallfan 执行运算：

$$K_{2} = A^{b} \bmod{p}$$

因为离散对数的幂运算有交换律， Smallfan 得到的结果也是 K，即：

$$K = A^{b} \bmod{p} = (g^{a} \bmod{p})^{b} \bmod{p} = g^{ab} \bmod{p} = (g^{b} \bmod{p})^{a} \bmod{p} = B^{a} \bmod{p}$$

这个 K 就是 Jenning 和 Smallfan 之间用的对称加密密钥，可以作为会话密钥使用。这也是

可以看到，整个密钥协商过程中， Jenning 和 Smallfan 公开了 4 个信息：P、G、A、B，其中 P、G 是算法的参数，A 和 B 是公钥，而 a、b 是双方各自保管的私钥，攻击者无法获取这 2 个私钥，因此攻击者只能从公开的 P、G、A、B 入手，计算出离散对数（私钥）。

思考题：为什么 Jenning 、 Smallfan 计算的 公钥=G^私钥 mod p 而不是 公钥=G^私钥 ？

4.2 与RSA对比

RSA的解决思路是：公钥加密，私钥解密。而DH密钥交换，是双方生成相同的密钥。即：共享密钥。虽然名字上叫密钥交换，但实际上，双方并没有真正交换密钥，而是通过计算生成出一个相同的共享密钥。因此，更确切叫法应该是Diffie-Hellman密钥协商。

4.3 敏感的私钥

DH诞生以后，常用的是 static DH 算法，所谓 static 即为一方的私钥是静态的。也正因为这个特性，一旦私钥泄露，DH算法便不具备前向安全性，所以目前DH算法已经被废弃了；

4.4 DHE算法

既然 static DH 算法中，一方固定一方临时生成的方式不安全，那么可以采用双方都不固定，通讯双方的私有密钥都采用临时生成的方式，这种DH算法便称之为 DHE算法（E是指Ephemeral, 临时的）。DHE算法 基于 DH算法，将不再赘述生成过程。

五、ECDHE原理

5.1 ECC算法

5.1.1 亟待解决的性能问题

由于 DHE算法 每次需要生成底数G和模数P，并对G进行多阶运算即乘法运算，在HTTPS高并发通信场景下对于CPU的负载非常大，于是 使用椭圆曲线（ECC）的 DH（Diffie-Hellman）算法（简称ECDHE算法） 孕育而生，要了解ECDHE算法，首先需要了解 椭圆曲线加密算法(ECC) 。

5.1.2 什么是ECC

ECC是Elliptic Curve Cryptography（椭圆曲线密码学）的缩写，是一种基于椭圆曲线数学的公开密钥加密算法，其本质是利用离散对数问题实现加密。ECC的主要优势，是在使用更小的密钥的同时，提供更快的性能和更高等级的安全。

5.1.3 什么是椭圆曲线

Wolfram MathWorld 给出了非常精准的定义：
一条椭圆曲线就是一组被 y^2 = x^3 + ax + b 定义的且满足 4a^3 + 27b^2 ≠ 0 的点集。
4a^3 + 27b^2 ≠ 0 这个限定条件是为了保证曲线不包含奇点（在数学中是指 曲线上任意一点都存在切线）。

椭圆曲线示例图：

5.1.4 离散对数问题

前文中有提到离散对数问题，并解释RSA算法基于大数的质因数分解，即对两个质数相乘容易，而将其合数分解很难的这个特点进行加密。

而ECC算法是在有限域Fp定义公式：Q=kP，已知大数k和点P的情况下，很容易求点Q，但是已知的点P、点Q，却很难求得k，ECC算法同样利用离散对数特点进行加密，点Q为公钥，大数k为私钥，点P为基点，和RSA最大的实际区别，主要是密钥长度。

5.1.5 椭圆曲线加密算法原理

描述一条Fp上的椭圆曲线，常用到六个参量：T=(p,a,b,n,x,y)。
（p 、a 、b） 用来确定一条椭圆曲线，p为素数域内点的个数，a和b是其内的两个大数；
x,y 为G基点的坐标，也是两个大数；
n为点G基点的阶；
以上六个量就可以描述一条椭圆曲线，有时候我们还会用到h(椭圆曲线上所有点的个数p与n相除的整数部分)。

现在我们描述一个利用椭圆曲线进行加密通信的过程：

1. 选定一条椭圆曲线 Ep(a,b) 并取椭圆曲线上一点，作为基点P。
2. 选择一个大数k作为私钥，并生成公钥 Q=kP。
3. 将 Ep(a,b) 和点Q、P传给用户。
4. 用户接到信息后 ，将待传输的明文编码到Ep(a,b)上的一点M，并产生一个随机整数r。
5. 公钥加密（密文C是一个点对）：C={rP, M+rQ}
6. 私钥解密（M + rQ - k(rP) ，解密结果就是点M），公式如下：

M + rQ - k(rP) = M + r(kP) - k(rP) = M

7. 对点M进行解码就可以得到明文。

假设在加密过程中，有一个第三者H，H只能知道椭圆曲线 Ep(a,b)、公钥Q、基点P、密文点C，而通过公钥Q、基点P求私钥k或者通过密文点C、基点P求随机数r都是非常困难的，因此得以保证数据传输的安全。

关于 椭圆曲线和阿贝尔群(abelian group) 的其他描述，本文不作展开。

5.2 基于ECDHE的密钥协商

ECDHE 算法是在 DHE 算法的基础上利用了 ECC 椭圆曲线特性，可以用更少的计算量计算出公钥，以及最终的会话密钥。

Jenning 和 Smallfan 使用 ECDHE 密钥交换算法的过程：

• 双方事先确定好使用哪种椭圆曲线，和曲线上的基点 G，这两个参数都是公开的；
• 双方各自随机生成一个随机数作为私钥d，并与基点 G相乘得到公钥Q（Q = dG），此时 Jenning 的公私钥为 Q1 和 d1， Smallfan 的公私钥为 Q2 和 d2；
• 双方交换各自的公钥，最后 Jenning 计算点（x1，y1） = d1Q2， Smallfan 计算点（x2，y2） = d2Q1，由于椭圆曲线上是可以满足乘法交换和结合律，所以 d1Q2 = d1d2G = d2d1G = d2Q1 ，因此双方的 x 坐标是一样的，所以它是共享密钥，也就是会话密钥。

这个过程中，双方的私钥都是随机、临时生成的，都是不公开的，即使根据公开的信息（椭圆曲线、公钥、基点 G）也是很难计算出椭圆曲线上的离散对数（私钥）。

六、基于ECDHE的TLS

6.1 Why ECDHE

TLS握手的核心目的在于密钥交换，服务器与客户端“协商”得出主密钥（所谓“协商” 就是互相交换几个随机数，你说一个数，我说一个数，最后根据大家的数计算出一个结果）。

不论RSA还是ECDHE，最终计算主密钥的公式都是相同的：

Client Random + Server Random + pre-master = master secret

前两个随机数完全明文，保密的关键在于 pre-master。

• 在RSA中，pre-master 是单纯的由客户端生成，通过服务器的公钥加密后发给服务器，服务器使用私钥解密拿到 pre-master。一旦服务器的私钥被破解，主密钥就会被攻击者算出，并且会导致过往的主密钥泄漏（RSA不具备“向前安全性”）。

• 在ECDHE中，服务器生成一个 “椭圆曲线的公钥” Server Params，对应公式中的A，使用私钥加密后将其发送给客户端；客户端也生成一个“椭圆曲线的公钥” Client Params，对应公式中的B，使用服务器的公钥加密后发给服务器；而私钥 a 和 b 由服务器和客户端分别保管。随后客户端与服务器分别在本地计算 pre-master：

在客户端上： A ^ b % P = Server Params ^ b % P = pre-master
在服务器上： B ^ a % P = Client Params ^ a % P = pre-master

由此可见，在ECDHE中，即使破解了服务器的私钥，拿到的也只是客户端发送的 Client Params，没有椭圆曲线的私钥a和b，就无法计算出 pre-master。

就算攻击者的算力强大，能够进一步破解出椭圆曲线的私钥，但每次密钥协商时服务器与客户端都是使用椭圆曲线随机生成私钥的，因此ECDHE算法具备前向安全性。

6.2 四次握手

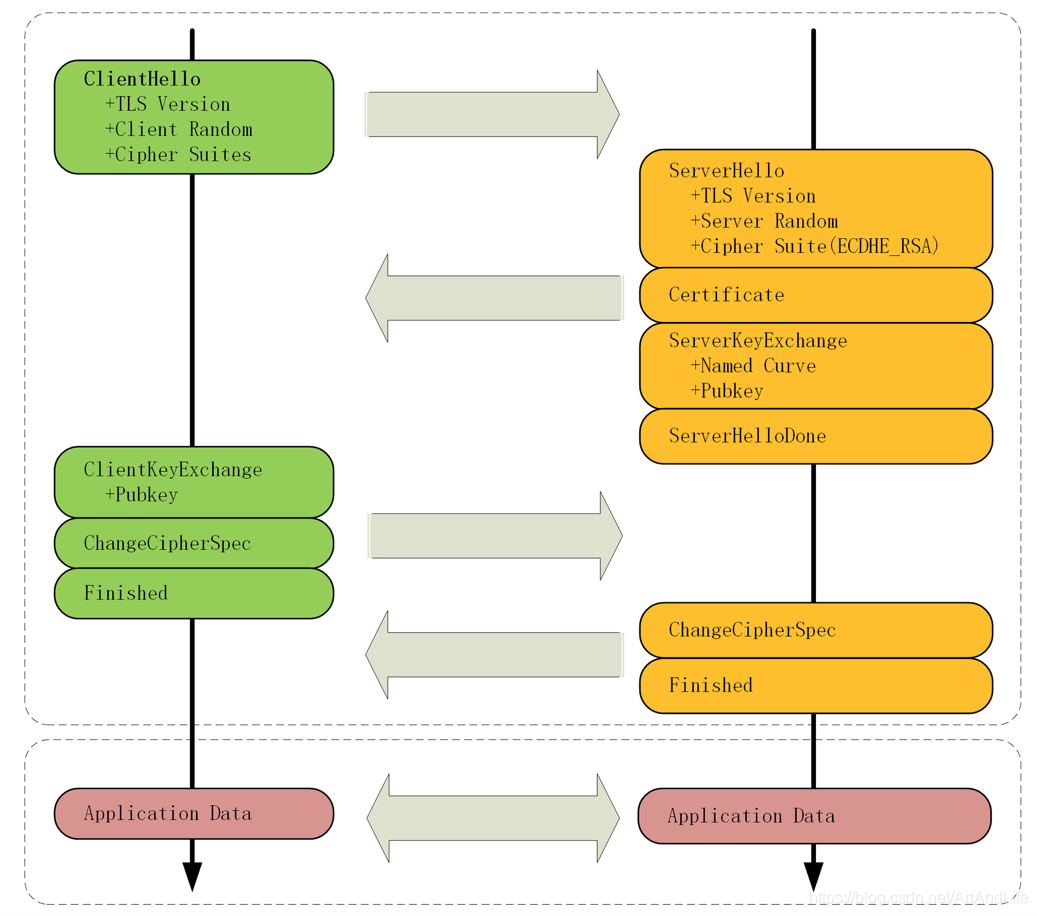
6.2.1 TLS第一次握手

客户端首先会发一个「Client Hello」消息，消息里面有客户端使用的 TLS 版本号、支持的密码套件列表，以及生成的 随机数（Client Random）。

6.2.2 TLS第二次握手

服务端收到客户端的「打招呼」，同样也要回礼，会返回「Server Hello」消息，消息面有服务器确认的 TLS 版本号，也给出了一个随机数（Server Random），然后从客户端的密码套件列表选择了一个合适的密码套件，此时密钥协商算法选用 ECDHE。

接着，服务端为了证明自己的身份，发送「Certificate」消息，会把证书也发给客户端。

注意：这一步和 RSA 握手过程有很大的区别：因为服务端选择了 ECDHE 密钥协商算法，所以会在发送完证书后，发送「Server Key Exchange」消息。

这个过程服务器做了三件事：

1. 选择对应的一种椭圆曲线，选好了椭圆曲线相当于椭圆曲线基点 G 也定好了，这些都会公开给客户端；
2. 生成随机数作为服务端椭圆曲线的私钥，保留到本地；
3. 根据基点 G 和私钥计算出服务端的椭圆曲线公钥，这个会公开给客户端。

为了保证这个椭圆曲线的公钥不被第三方篡改，服务端会用 RSA 签名算法给服务端的椭圆曲线公钥做个签名。

随后，就是「Server Hello Done」消息，服务端跟客户端表明：“这些就是我提供的信息，打招呼完毕”。

至此，TLS 两次握手就已经完成了，目前客户端和服务端通过明文共享了这几个信息：Client Random、Server Random 、使用的椭圆曲线、椭圆曲线基点 G、服务端椭圆曲线的公钥，这几个信息很重要，是后续生成会话密钥的材料。

6.2.3 TLS第三次握手

客户端收到了服务端的证书后，通过 CA证书链 验证证书真实性后，生成一个随机数作为客户端椭圆曲线的私钥，然后再根据服务端前面给的信息，生成客户端的椭圆曲线公钥，然后用「Client Key Exchange」消息发给服务端。

至此，双方都有对方的椭圆曲线公钥、自己的椭圆曲线私钥、椭圆曲线基点 G。于是，双方都就计算出点（x，y），其中 x 坐标值双方都是一样的，前面说 ECDHE 算法时候，说 x 是会话密钥，但实际应用中，x 还不是最终的会话密钥。

最终的会话密钥，就是用「客户端随机数 + 服务端随机数 + x（ECDHE 算法算出的共享密钥） 」三个材料生成的。

之所以这么麻烦，是因为 TLS 设计者不信任客户端或服务器「伪随机数」的可靠性，为了保证真正的完全随机，把三个不可靠的随机数混合起来，以提高「随机」的程度。

接着，客户端会发「Encrypted Handshake Message」消息，把之前发送的数据做一个摘要，再用对称密钥加密一下，让服务端做个验证，验证下本次生成的对称密钥是否可以正常使用。

6.2.4 TLS第四次握手

最后，服务端也会有一个同样的操作，发「Change Cipher Spec」和「Encrypted Handshake Message」消息，如果双方都验证加密和解密没问题，握手正式完成，进入加密收发阶段。

6.3 性能

使用了 ECDHE，在 TLS 第四次握手前，客户端实际上可以进行加密 HTTP 数据的发送工作，而对于 RSA 握手过程，必须要完成 TLS 四次握手，才能传输应用数据。

ECDHE 相比 RSA 握手过程省去了一个消息往返的时间，这个有点「抢跑」的意思，它被称为是「TLS False Start」，跟「TCP Fast Open」有点像，都是在还没连接完全建立前，就发送了应用数据，这样便提高了传输的效率。

6.3.1 认识 TLS False Start

先看看 HTTP。在最不理想状况下，一个正常HTTP到达TTFB（Time To First Byte）需要经过以下过程：1个DNS查询RT、1个TCP握手RT，至少一个HTTP请求和响应RT。我们假设客户端和服务器之间的RTT为50ms（50ms也是中国网络从南到北延迟值），这里我们暂且不考虑DNS，所以在这个假设下，HTTP到达TTFB需要100ms。

再来看看HTTPS过程，相比于HTTP，HTTPS多出两个RTT用来协商TLS隧道（这里忽略加解密计算和OCSP等时间因素），同样不考虑DNS，在这个假设下，HTTPS到达TTTFB需要200ms。

可以看到，HTTPS通信时间是HTTP的整整两倍，这也是认为HTTPS慢的重要原因之一。

试想，如果能够减少HTTPS通信过程的RT，将时间从200ms提高到150ms，那直接减少了1/4的时间消耗，这对于高并发高负载的服务器性能提升和带宽节省是显而易见的。

这当然是有办法的。

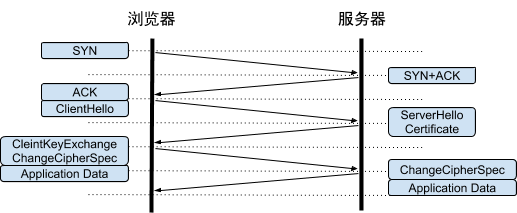
TLS False Start是 Google 提出来的优化方法，其做法是：在 TLS 协商第二阶段，客户端发送ChangeCipherSpec 和 Finished 后，立即发送加密的应用层数据，而无需等待服务器端的确认。

下图是启用TLS False Start之后的HTTPS通信过程。

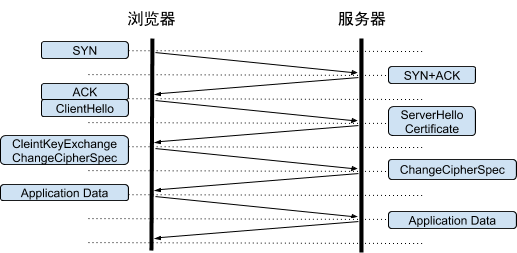
6.3.2 对比RSA

TLS 1.2 版本如果使用的是 RSA 密钥交换算法，那么需要 4 次握手，也就是要花费 2 RTT，才可以进行应用数据的传输。

因此如果可以，尽量选用 ECDHE 密钥交换算法（TLS 1.3版本使用）替换 RSA 算法，因为该算法由于支持「TLS False Start」，客户端可以在 TLS 协议的第 3 次握手后，第 4 次握手前，发送加密的应用数据，以此将 TLS 握手的消息往返由 2 RTT 减少到 1 RTT。

ECDHE 算法是基于椭圆曲线实现的，不同的椭圆曲线性能也不同，应该尽量选择 x25519 曲线，该曲线是目前最快的椭圆曲线。

6.3.3 TLS 1.3 优化

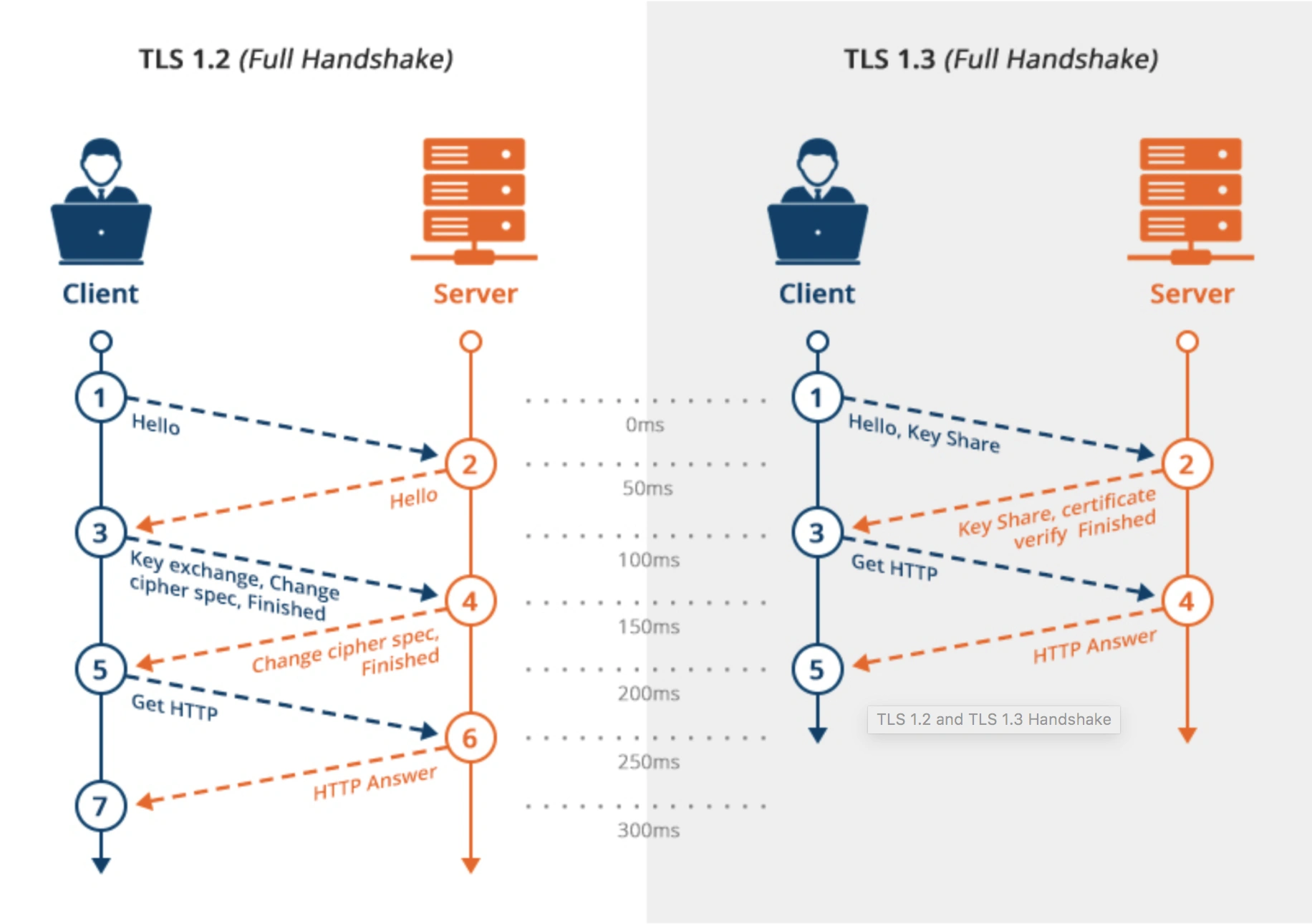
综上所述，如果可以，直接把 TLS 1.2 升级成 TLS 1.3，TLS 1.3 大幅度简化了握手的步骤，完成 TLS 握手只要 1 RTT，而且安全性更高。

在 TLS 1.2 的握手中，一般是需要 4 次握手，先要通过 Client Hello （第 1 次握手）和 Server Hello（第 2 次握手） 消息协商出后续使用的加密算法，再互相交换公钥（第 3 和 第 4 次握手），然后计算出最终的会话密钥，下图的左边部分就是 TLS 1.2 的握手过程：

上图的右边部分就是 TLS 1.3 的握手过程，可见 TLS 1.3 把 Hello 和公钥交换这两个消息合并成了一个消息，于是这样就减少到只需 1 RTT 就能完成 TLS 握手。

具体的做法是：

• 客户端在 Client Hello 消息里带上了支持的椭圆曲线，以及这些椭圆曲线对应的公钥。
• 服务端收到后，选定一个椭圆曲线等参数，然后返回消息时，带上服务端这边的公钥。经过这 1 个 RTT，双方手上已经有生成会话密钥的材料了，于是客户端计算出会话密钥，就可以进行应用数据的加密传输了。

另外需要注意：TLS 1.3废除了不支持前向安全性的 RSA 和 DH 算法，只支持 ECDHE 算法。

七、再谈量子计算

7.1 过去的假想

许多人担心量子计算机将能够破解某些用于发送安全信息的加密代码。所谓的加密代码使用“陷门（trapdoor）”函数加密数据，这种函数在一个方向上十分容易执行，但在相反方向上则不然（质因数分解、离散对数都是如此）。这就使得加密数据变得容易，但如果没有特殊密钥的帮助，解码数据就非常困难。

这些加密系统一直都不是牢不可破的。相反，它们的安全性是通过经典计算机完成解码所需的大量时间体现的。现代的加密方法是专门设计的，解码它们需要很长时间，因此说它们几乎不可破解。

但是量子计算机改变了这种想法。量子计算机比传统的计算机功能强大得多，应该能够轻松破解这些代码。

这就提出了一个重要的问题——量子计算机何时才能强大到可以做到这一点? 在此之后，受此加密形式保护的所有信息都将变得不安全。

因此，计算机科学家们试图计算出构建这样一台量子计算机可能需要的资源，以及构建这种机器需要多长时间。此前的答案总是几十年。

7.2 可怕的量子计算科学

早在 1994 年，美国数学家 Peter Shor 就发现了一种量子算法，其性能优于经典算法。Shor 的算法因子大，是破解基于陷门函数密码的关键因素。

陷门函数是基于乘法过程的，它在一个方向上很容易执行，但在相反的方向上很难执行。例如，将两个数字相乘很简单：593 乘以 829 等于 491,597。但是很难算出 491,597 是由哪两个质数相乘才能得到。

随着数字的增大，计算变得越来越困难。事实上，计算机科学家认为经典计算机几乎不可能分解出大于 2048 位的数字，而 2048 位是 RSA 加密最常用的基础形式。具体的 benchmark 可参考 量子计算机能在8小时内破解2048位RSA加密，本文不作展开。

Shor 证明，一个功能足够强大的量子计算机可以轻松做到这一点，这一结果在整个安全行业一石激起千层浪。

从那以后，量子计算机的功能一直在增强。2012 年，物理学家们用一台四量子位量子计算机来分解 143。然后在 2014 年，他们使用了类似的设备来分解出了 56153。

到了2019年，谷歌的 Craig Gidney 和瑞典斯德哥尔摩 KTH 皇家理工学院的 Martin Ekera 的研究报告【How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits】显示，这个答案需要被修正。Gidney 和 Ekera 已经展示了量子计算机如何用 2000 万个量子位来进行计算。他们证明，这样一个装置只需要 8 个小时就可以完成计算。他们表示：“这一结果，已经使得分解 2048 位 RSA 整数最多需要多少量子位，下降了近两个数量级。”

而就在最近的2022年12月，清华和浙大等中国研究人员在预印本平台 arxiv 上发表论文，报告破解2048位RSA密钥所需的量子比特数可以大幅减少，现有的量子计算机就能做到。如果验证属实的话，这项研究将标志着计算机安全史上的一个重要时刻：政府、军方和安全机构、银行证券以及所有需要保护数据将不再安全！ (新闻出处)

7.3 可能的替代算法

以BB84协议为代表的量子加密算法，这和经典的“一次一密”一样不可破解，而且还没有后者可能在交换密钥过程中的极大风险性。关于量子密钥分发，笔者了解不深，不作误导，遂待后续可能深入后再谈。

参考文献
小林Coding - 3.5 HTTPS 如何优化？
阮一峰的网络日志 - RSA算法原理（一）
阮一峰的网络日志 - RSA算法原理（二）
TLS False Start究竟是如何加速网站的
挥之不去的“经典”——关于BB84量子密钥分发协议（一）